가속도 센스 활용(1) - 이동 거리 산출법
페이지 정보
작성자 티앤에이치 댓글 0건 조회 6,668회 작성일 18-12-08 19:51본문
가속도 센스는 많이 나와 있지만 이를 활용하는 부분에서 머뭇거릴때가 있다.
가속도 값을 주기적으로 연속 측정할때 마다 거리와 속도를 구해야하는데,
이 때 아래 단 한 줄의 최종 공식을 활용하면 쉽게 접근 할 수 있다.
1. 기본공식
S= V0*t + (a*t^2/2)
a=(V-V0)/t , V=a*t + V0
2. 가속도에서 속도 구하기 - (이동 거리를 구하는데 무관함,참조용)
V1=a1*(t1-t0) + V0 ------------------------------(a)
시간 간격이 일정하다면, td=tn - t(n-1) = .... = t2 - t1 = t1-t0
V2=a2*(t2-t1) + V1
=a2*(t2-t1) + a1*(t1 - t0) + V0
=(a2+a1)td+V0
=a2*td + V1
V3=a3*(t3-t2) + V2
=a3*(t3-t2) + a2*(t2-t1) + a1*(t1 - t0) + V0
=a3*td + a2*td + a1td +V0
=a3*td + V2
V3=(a3+a2+a1)*td + V0
V(n) = (an+a(n-1)+...+a1) * td + V0
=an*td + V(n-1)
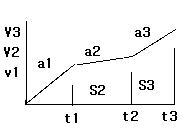
3. 이동 거리 구하기
S1= (a1*td^2)/2 + V0*td
S2= (a2*td^2)/2 + V1*td --------------- (b) -----> V1에 (a)식을 대입함
= (a2*td^2)/2 + (a1*td + V0)*td
= (a2*td^2)/2 + a1*td^2 + V0*td -----> a1*td^2를 2개로 분리함
= (a2*td^2)/2 + (a1*td^2)/2 + (a1*td^2)/2 + V0*td -----> (a1*td^2)/2 + V0*td 는 S1과 동일
= (a1*td^2)/2 + (a2*td^2)/2 + S1
= (a1 + a2)*td^2/2 + S1
S3= (a3*td^2)/2 + V2*td -----> V2에 (a)식을 대입함
= (a3*td^2)/2 + (a2*td+ V1)*td
= (a3*td^2)/2 + a2*td^2 + V1*td
= (a3*td^2)/2 + a2*td^2/2 + a2*td^2/2 + V1*td ---------> 식(b)를 대입
= (a3*td^2)/2 + a2*td^2/2 + S2
= (a2 + a3)*td^2/2 + S2
이와 같이 하여 아래의 최종식을 얻을 수 있다.
S(n) = S(n-1) + (a(n-1) + a(n))*td^2/2 -->최종 적용공식
* 매 순간의 이동거리는 이전 이동거리와 이전의 가속도, 현재의 가속도로 산출이 가능하다.
순간이동거리를 계속 누적 시키면 총이동거리를 산출 할 수 있다.
거리의 산출은 속도,가속도,이동거리가 '0' 인 최초 정지 상태에서 시작해야 하므로,
가속도계의 상태와 기타 환경변수를 가지고 시작점(정지 상태)을 정의하고 그 시점부터 산출하여야 한다.
이 방식은 시작점으로부터 멀어질 수록 누적오차가 커지는 단점이 있어 이를 보완하기 위한 여러가지 조치가 필요하다.
(이 부분은 다음장에서~)
위와 같이 순간 이동거리에서 누적시키지 않고 순간 가속도로 바로 누적거리 산출하는 방식은 아래와 같다.
조건 : T= td^2 라함, S는 순간 이동거리 , S'는 누적이동거리
S0=0
S1'= S1+0=a1/2*T
S2' = S2+S1'
= (a2/2*T + a1/2*T) + S1 + S1
= 1a2/2*T +3a1/2*T
S3'=S3+S2'= (a3/2*T + a2/2*T) + S2 + S2 + S1'
= (a3/2*T + a2/2*T) + 2(a2/2*T + a1/2*T) + 2S1 + S1
= a3/2*T + 3a2/2*T + 2a1/2*T + 2a1/2*T + a1/2*T
= a3/2*T + 3a2/2*T + 5a1/2*T
=(a3 + 3a2 + 5a1)/2*T
S4'=S4+S3'=S4+S3+S2'=S4+S3+S2+S1'=
= (a4/2*T + a3/2^T) + S3 + S3 +S2 + S1'
= (a4/2*T + a3/2^T) + 2(a3/2*T + a2/2*T) + 3S2 +S1
= (a4/2*T + a3/2^T) + 2(a3/2*T + a2/2*T) + 3(a2/2*T +a1/2*T) +4S1
= a4/2*T+ 3a3/2^T +2a2/2*T + 3a2/2*T + 3a1/2*T + 4a1/2*T
= a4/2*T+ 3a3/2^T +5a2/2*T + 7a1/2*T
=(a4 + 3a3 + 5a2 + 7a1)/2*T
S4'-S3'= (a4 + 3a3 + 5a2 + 7a1)/2*T - (a3 + 3a2 + 5a1)/2*T
= (a4+ 2a3 + 2a2+2a1)/2*T
S4'=(a4/2+a3+a2+a1)/2*T + S3'
'와>
댓글목록
등록된 댓글이 없습니다.